跳到主要内容

剑指 Offer II 051.节点之和最大的路径

· 阅读需 4 分钟

1、题干​

路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给定一个二叉树的根节点 root ，返回其 最大路径和，即所有路径上节点值之和的最大值。

 

示例 1：

输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

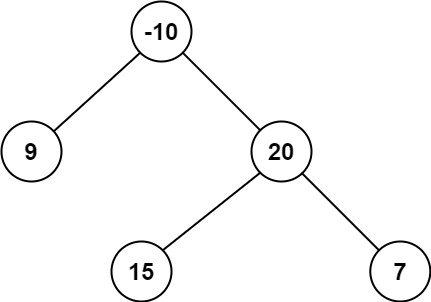
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

 

提示：

  • 树中节点数目范围是 [1, 3 * 104]
  • -1000 <= Node.val <= 1000

 

注意：本题与主站 124 题相同： https://leetcode-cn.com/problems/binary-tree-maximum-path-sum/

2、解题思路​

深度遍历树上所有节点，对每个节点求最大路径和即可。

3、代码​

var maxPathSum = function (root) {
    let res = root.val;
    function dfs(node) {
        if (!node) return -Infinity;
        const maxSum1 = dfs(node.left), maxSum2 = dfs(node.right);
        const maxSum = Math.max(node.val, maxSum1 + node.val, maxSum2 + node.val);
        res = Math.max(res, maxSum, maxSum1, maxSum2, maxSum1 + maxSum2 + node.val);
        return maxSum;
    }
    return dfs(root), res;
};

关键代码说明

  • 求每个节点的最大路径和，且路径不重复的关键
    • const maxSum = Math.max(node.val, maxSum1 + node.val, maxSum2 + node.val);
    • 这行代码用于求当前节点下的最大路径和maxSum，并将其返回给父节点用于计算父节点下的最大路径和
    • Math.max取最大值时包含当前节点的值、当前节点值+左子节点最大路径和、当前节点值+右子节点最大路径和
    • 即最大路径和一定要包含当前节点的值，还可能叠加某个子节点最大路径和，也可能不叠加子节点最大路径和
    • 因此dfs函数逐级返回时，由下至上形成了一条不分叉的路径，并能逐级向上返回子节点的最大路径和
  • 求整棵树最大路径和res的关键
    • res = Math.max(res, maxSum, maxSum1, maxSum2, maxSum1 + maxSum2 + node.val);
    • 在每个节点求最大路径和时，res取其自身以及maxSum1、maxSum2、node.val三者任意组合的路径和中的最大值
    • maxSum1、maxSum2、node.val三者任意组合求和时，至少取1个，且取2个时不能是maxSum1 + maxSum2，因为这个组合不构成路径

4、执行结果​

1.png